| |
Una delle conseguenze più strabilianti che
Einstein fa risalire alla sua teoria della relatività è la celebre equazione
E = m c2
[Questa equazione era stata trovata
precedentemente da Poincarrè e da Olinto del Pretto del tutto
indipendentemente dalla teoria della relatività .]
Questa formula, come d’altronde tutta la teoria
della relatività ristretta è una diretta conseguenza della spiegazione
dell’effetto fotoelettrico, ed infatti l’articolo che riguarda l’effetto
fotoelettrico, quello che riguarda la relatività ristretta e quello che
riguarda l’equivalenza tra la massa e l’energia vengono pubblicati nello
stesso anno (1905).
Come già detto nella trattazione dell’effetto
fotoelettrico Einstein abbraccia completamente la teoria della natura
corpuscolare della luce, già ipotizzata da Newton, ed applica la meccanica
classica alla trattazione del moto del fotone che identifica come la
particella fondamentale della luce.
Egli accetta le equazioni di Maxwell che
conducono alla definizione della velocità della luce come una costante
universale, tuttavia per poter giustificare la natura corpuscolare della
radiazione, e quindi ricondurre la sua trattazione all’interno della
meccanica classica egli è costretto ad una completa ridefinizione dei
concetti fondamentali di spazio e di tempo che da variabili indipendenti,
assumono la funzione di variabili dipendenti dalla velocità del sistema di
riferimento.
Abbiamo visto che il principio di relatività di
Galileo è una diretta conseguenza del principio di conservazione
dell’energia che Einstein utilizza ampliamente all’interno della sua
teoria ma che è costretto ad abbandonare quando postula la costanza della
velocità del fotone.
Vediamo con quale procedura Einstein ricava la sua formula.
Nel lavoro pubblicato il 30 giugno 1905 ( on the electrodynamics of moving bodies), attraverso l’applicazione delle
trasformazioni di Lorentz alle Equazioni di Maxwell-Hertz perviene alla relazione
W= mc2 [γ -1]
Cioè fa derivare la nota formula direttamente
dalla sua teoria della relatività, assumendosene quindi direttamente la
paternità con tutte le conseguenze ad essa correlate all’interno della sua
teoria.
Il procedimento che egli utilizza consiste nel riscrivere le equazioni di Maxwell-Hertz
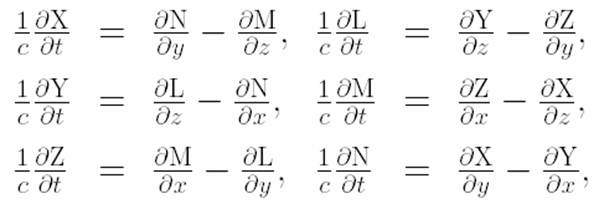
utilizzando un sistema di coordinate in movimento rettilineo uniforme
lungo l’asse x con velocità v rispetto a quello fisso a cui ha applicato
le trasformazioni di Lorentz trovate precedentemente. In tal modo perviene
alle relazioni
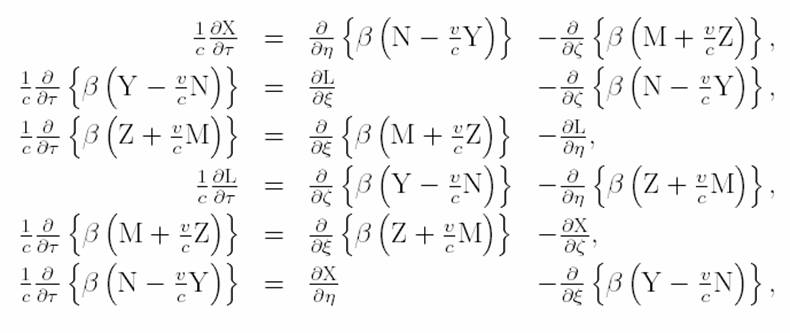
in cui si nota chiaramente che si
perdono completamente le relazioni di ortogonalità tra il campo elettrico
ed il campo magnetico vanificando in un certo qual modo tutto il lavoro di
Maxwell e degli altri fisici che è rivolto a cercare le invarianze e non
le covarianze, infatti la derivata rispetto al tempo della componente del
campo elettrico X non dipende esclusivamente dalle componenti del campo
magnetico N ed M ma anche dalle altre componenti del campo elettrico Y e
Z.
Successivamente egli impone, per il principio di relatività, l’equivalenza
formale di dette espressioni con quelle generiche espresse nel sistema di
coordinate mobili
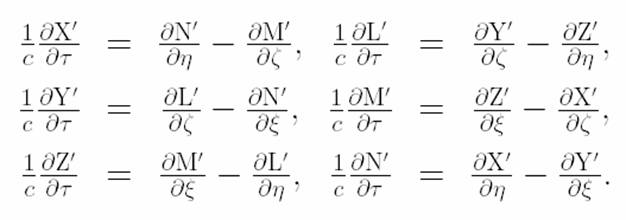
sia nel passaggio dal sistema di riferimento fisso a quello mobile che nel
processo inverso e perviene alle seguenti corrispondenze tra le componenti
del campo elettromagnetico nei due sistemi
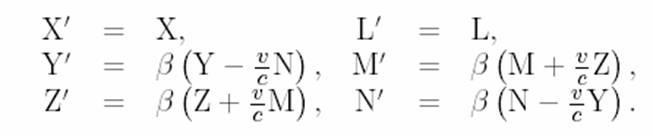
In questo modo Einstein riesce a mantenere
invariate le componenti del campo elettrico X e magnetico L lungo la
direzione dello spostamento degli assi ma a causa delle proprietà del
rotore vengono inevitabilmente rimescolatele altre quattro componenti del
campo elettromagnetico Y , Z, M, N.
Le proprietà del rotore sono inoltre tali che la forza che agisce lungo
l’asse di spostamento del sistema di coordinate è determinata anche dalle
componenti del campo elettrico ( e magnetico) perpendicolari a tale asse,
tale considerazione viene del tutto ignorata da Einstein nella
determinazione dell’energia cinetica di un elettrone lungo l’asse di
traslazione delle coordinate e comporta che la relazione
W= mc2 [γ -1],
che egli determina , sia non valida.
Nella successiva nota del 27 Settembre dello stesso anno, nonostante le affermazioni poste
all’inizio, Einstein abbandona la strada delle equazioni di Maxwell per
dimostrare la sua formula e prende in considerazione un corpo
con energia E0 posto all’origine O di un sistema a riposo S di
assi cartesiani che emette nella direzione positiva e negativa dell’asse
x due onde piane luminose uguali di energia ciascuna ½ L ; se l’energia
dopo l’emissione avrà il valore E1 allora le tre quantità
saranno, per il principio di conservazione dell’energia, legate dalla
relazione:
E0 = E1 +½ L+½ L = E1+L
Se mettiamo infatti ad una certa distanza dall’origine degli assi , nella parte positiva e nella parte
negativa dell’asse x due osservatori vediamo che essi registrano la stessa
frequenza e quindi, per la relazione E= h ν la stessa energia.
A questo punto introduce un nuovo sistema di riferimento S' ( aggiungiamo noi analogo al sistema S e cioè
con i due osservatori messi nella stessa posizione) che è in moto uniforme
lungo la direzione positiva dell’asse x con la velocità v, e vuole
osservare il fenomeno di emissione appena descritto da questo nuovo
sistema di riferimento. Chiamando H0 ed H1 i valori
dell’energia in questo nuovo sistema di riferimento prima e dopo
l’emissione abbiamo che:
H0 = H1 +½ L(1-v/c) +½ L(1+v/c) = H1+L
Il valore +½ L(1-v/c) può essere determinato dall’osservatore posto sull’asse
positivo del sistema S' che misura la frequenza della luce proveniente da O (caso CB2 nel
capitolo ) ed analogamente per il valore +½L(1+v/c) (caso CB1) .
Sottraendo le due espressioni abbiamo
H0 - E0 - (H1 - E1) = 0
Cioè come è ben noto dalla meccanica classica l’energia di un sistema è una grandezza
invariante che non dipende dal sistema di riferimento ( principio di
conservazione dell’energia).
Il sistema che utilizza Einstein invece è quello di introdurre il fattore di
normalizzazione γ
derivato dalle trasformazioni di Lorentz che gli permette di mantenere
costante la velocità della luce ( considerata come particelle, cioè come
fotoni) ma che non soddisfa il principio di conservazione dell’energia ,
infatti la precedente differenza, considerando l’energia cinetica, diventa
diversa da zero cioè:
K0 - K1 = L ( γ -1) =L [ 1/(1-v2/c2)½ - 1]
Che egli approssima al primo termine della sviluppo in serie
K0 - K1 = ½ (L/c2)v2
La formula precedente è del tutto
simile alla forma classica dell’energia cinetica una volta posto che sia
m= L/c2 che lo porta a concludere
che “If a body gives off the energy L in the
form of radiation, its mass diminishes by L/c2. …… so that we
are led to the more general conclusion that the mass of a body is a
measure of its energy-content…..”.
Questa conclusione è viziata, oltre che dall’illecita introduzione del fattore di normalizzazione γ
anche dalla constatazione che l’approssimazione adottata può avere significato solo per piccoli valori
di v cioè quando siamo vicini al caso classico e quindi non c’è bisogno di γ mentre quando γ
assume significato, cioè in condizioni relativistiche, l’approssimazione
non è più valida. Quindi l’equazione E=mc2 che egli ritiene di
aver trovato tramite la teoria della relatività è valida solo nel caso
classico, cioè quando la teoria della relatività non è necessaria.
Una successiva espressione di questa
formula viene fornita da Einstein in un articolo divulgativo della
relatività edito nel 1916 in cui inserisce la formula all’interno della
definizione dell’energia di un corpo materiale
E= mc2 γ = mc2 (1-v2/c2)-1/2
Che fermata al secondo termine dell’espansione in serie binomiale da
E= mc2 +1/2 mv2
Ci sono state altre derivazioni di questa famosa formula, prima della
formulazione della teoria di Einstein ( Olinto del Pretto e Poincaré ) e
successive ad essa Eric Baird ed altri. Il comune denominatore di tutte
queste determinazioni, comprese quelle di Einstein, è costituito dal fatto
che tutti considerano il fotone come una particella materiale dotata di un
proprio momento della quantità di moto ed a cui applicano le leggi della
meccanica classica. Osservata da questo punto di vista allora la
derivazione della formula diventa banale, infatti se consideriamo un tubo
metallico con al centro una carica esplosiva ed ai lati due proiettili di
massa m ciascuno, dopo l’esplosione, per il principio di conservazione
della quantità di moto e trascurando gli effetti di riscaldamento,
l’energia liberata della reazione chimica che determina l’esplosione si
trasforma nell’energia cinetica dei due proiettili per cui
E= ½ mv2 + ½ mv2 = mv2
Se facciamo un analogo esperimento con una sostanze che emette fotoni essendo c la velocità della luce avremo
E= ½ mc2 + ½ mc2 = mc2
La relazione E=mv2 è in pratica quella che
definisce la massa inerziale, cioè a parità di energia, la massa m è
inversamente proporzionale al quadrato della velocità v2 ;
naturalmente se noi teniamo costante la velocità v per vari proiettili
allora dovremmo fornire a ciascuno di essi una energia proporzionale alla
sua massa. Cioè la massa m di un proiettile è quella che impedisce allo
stesso di raggiungere una velocità infinita.
Per quanto riguarda il fotone invece dovremmo ammettere che
la sua massa non sia di tipo inerziale perché la velocità della luce è
costante e dovremmo associare ad ogni fotone di un diverso colore una
massa proporzionale alla frequenza della radiazione collegata, cioè un
fotone ultravioletto (λ = 250 nm) ha
una massa doppia di un fotone giallo ((λ = 500 nm).
Noi sappiamo dalla meccanica quantistica che l’emissione
di un fotone è dovuto alla transizione di un elettrone ( che non varia la
sua massa) da un livello atomico o molecolare a più alta energia ad un
livello ad energia minore, durante il processo di emissione vi è quindi
una variazione di energia dell’atomo o della molecola in esame ma nessuna
variazione della sua massa. L’emissione del fotone tuttavia è collegata
allo spostamento di una particella carica, con una sua massa
caratteristica, all’interno di un atomo o di una molecola, ma la sua
propagazione nello spazio non comporta nessun trasferimento di massa (sia
dal punto di vista sperimentale, che dal punto di vista teorico della
meccanica quantistica) ma esclusivamente un trasferimento di energia
dovuta alla variazione del momento di dipolo dell’atomo o della molecola
secondo le leggi dell’elettrodinamica classica descritte dalle equazioni
di Maxwell-Hertz.
Una riprova di quanto detto l’abbiamo se
consideriamo un fotone nella zona del medio infrarosso, dove l’emissione è
dovuta alle vibrazioni molecolari, cioè allo spostamento di nuclei atomici
più o meno carichi elettricamente all’interno di una molecola. In questo
caso è previsto teoricamente e confermato sperimentalmente che l’energia
del fotone è inversamente proporzionale alla massa degli atomi che lo
generano.
Se quindi non entriamo nel campo della fisica
nucleare o della fisica delle alte energie l’espressione E = mc2,
ottenuta per illecita trasposizione dalla relazione E = mv2,
non ha nessun significato né nel campo fisico-sperimentale né nel campo
teorico-filosofico-razionale.
La spiegazione dell’effetto fotoelettrico
fornita da Einstein, che per altro è stata fondamentale per lo sviluppo
della meccanica quantistica, ha cercato di ricondurre la teoria
elettromagnetica nel campo della meccanica classica assegnando al fotone
un momento di quantità di moto. In questa sua operazione egli era
completamente in linea con l’opinione corrente della scienza a cavallo
del XIX e XX secolo che aveva completamente abbandonato l’ipotesi dell’
“etere luminifero” abbracciata da Maxwell e dallo stesso Lorentz nella
formulazione della loro teoria elettromagnetica.
Questo abbandono era la conseguenza di una
illecita interpretazione dell’esperimento interferometrico del 1887
compiuto da A. Michelson ed E. Morley che erano alla ricerca di un
“ effetto vento” determinato da quell’ “etere” a cui era stata assegnata
dai suoi sostenitori, a partire da Cartesio, una natura “materiale” cioè
di un fluido più o meno denso composto da particelle di massa propria.
L’interpretazione dell’effetto Doppler ( acustico ed ottico) ci ha
permesso nei precedenti capitoli di stabilire che l’esperimento
interferometrico del 1887 non era in grado di stabilire nessun effetto di
movimento del sistema di riferimento rispetto all’etere proprio per la
ragione che sia l’emettitore di luce che il rivelatore avevano la stessa
energia intrinseca perché si trovavano solidali con
la superficie terrestre e perché, come ci mostra la meccanica quantistica,
la natura dell’ ”etere luminifero” non è di tipo materiale come quello
che trasmette le onde sonore ma esclusivamente di tipo energetico (
potenziale), cioè di tipo elettromagnetico.
La nozione di campo
elettromagnetico, come pure quella di campo gravitazionale, è oggi
accettata da tutta la comunità scientifica senza per questo inficiare il
valore del lavoro di Einstein sull’effetto fotoelettrico che va
interpretato non attraverso la quantizzazione del campo elettromagnetico
(che fra l’altro è smentita dallo stesso effetto Doppler in cui l’energia
della radiazione, cioè del fotone, varia con continuità in funzione dell’energia
intrinseca, cioè traslazionale, dell’apparato emettitore o rivelatore)
ma attraverso la quantizzazione del processo atomico-molecolare che causa
la variazione del dipolo atomico-molecolare che a sua volta causa la
polarizzazione del campo elettromagnetico e si trasmette nello spazio
attraverso le leggi dell’elettrodinamica.
Naturalmente questa
trattazione non è completa perché manca tutta la parte della fisica
nucleare dove sembra tra l’altro che l’equazione E= mc2 abbia
trovato le maggiori ed inconfutabili conferme; le energie in gioco nei
processi di fissione e fusione nucleare sono estremamente più elevate e
la natura ondulatoria delle radiazioni ( alfa, beta ecc. ) è più
strettamente legata agli aspetti probabilistici che agli aspetti
elettromagnetici. La fisica nucleare quindi richiederebbe una trattazione
a parte tuttavia quello che risulta dalla presente trattazione è che la
formula E = mc2 , non è correlata con la teoria della
relatività di Einstein e non ne costituisce una sua conferma.
|
|